Prima di analizzare i risultati dell’analisi non lineare, si riassumono quelli del calcolo manuale nell’immagine seguente:

Dalla valutazione svolta si evince come la puntellazione si ribalti non appena si attivi anche una piccola quota della forza sismica, che nell’esempio è calcolata sulla base della risultante della distribuzione triangolare di forze lungo l’altezza (cfr. NTC2018 §7.3.4.2, distribuzioni Gruppo 1).

Passiamo ora all’analisi dei risultati della statica non lineare, cominciando dalle reazioni al piede. La storia di carico settata in precedenza prevedeva l’applicazione del peso proprio della struttura in 10 passi, in un tempo da t=0s a t=1s.

La somma delle reazioni che otteniamo a t=1s è il peso proprio della struttura di puntellazione (13.11kN, molto simile alla stima pari a 13.5kN mostrata in precedenza).

Tutte le reazioni di figura precedente sono rivolte verso l’alto perché tutte le basette sono compresse. Per t=1.1s, cioè il passo corrispondente all’applicazione del 10% delle forze laterali, le reazioni cambiano come segue:

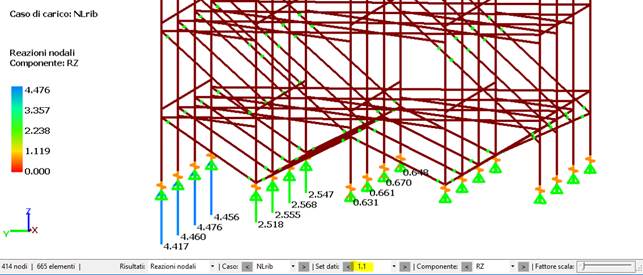
e cioè le basette a destra vanno in trazione. La situazione peggiora al 20% del carico (t=1.2s), come mostrato in figura seguente.

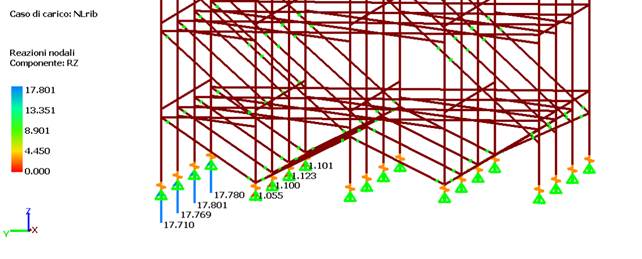
La distribuzione delle reazioni di compressione è triangolare, e non si vedono mai trazioni grazie alle molle di tipo gap, che reagiscono solo alla compressione permettendo alla basetta di sollevarsi.

Il risultato più interessante è sicuramente la deformata dell’analisi. Per t=1.2s, la deformata mostra chiaramente come le basette di sinistra si sollevino, mentre l’ultima fila di basette a destra faccia da perno.

Si ribadisce che in un analisi lineare avremmo visto le trazioni ai vincoli. Per un’analisi lineare con pesi propri al 100% e le forze laterali al 20% otteniamo le seguenti reazioni di trazione:

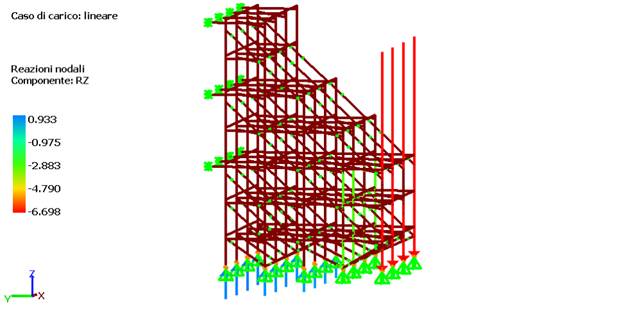
L’analisi non lineare è quindi uno strumento molto potente in grado di fornire risposte molto più aderenti alla realtà di quanto non possano fare le analisi lineari comunemente utilizzate nella pratica.