L’analisi dinamica modale, detta anche analisi con spettro di risposta (RS), permette di ottenere il massimo valore delle forze, degli spostamenti e delle reazioni vincolati di una struttura, partendo da uno spettro di progetto definito in termini di periodo T contro pseudo-accelerazioni Sa. Lo spettro di progetto è, in genere, fornito dalle norme di progettazione.
L’equazione del moto coinvolge la matrice di massa 
, la matrice di rigidezza 
e la matrice di smorzamento 
.
(1)
Nell’Eq. 1, 
è il vettore di
spostamento che vogliamo trovare come soluzione del sistema, 
è il vettore di trascinamento, che
specifica in quali direzioni dello spazio agisce l’accelerazione al suolo 
applicata.
La base per lo spazio di tutte le possibili configurazioni
deformate può essere descritta combinando linearmente gli autovettori 
che possono essere estratti dal
sistema
(2)
essendo 
il quadrato
della frequenza ciclica per ogni modo di vibrare, e 
la
matrice identità.
Conseguentemente, lo spostamento può essere scritto come
prodotto fra la matrice che raccoglie tutti gli autovettori normalizzati 
e le coordinate modali 
.
(3)
Sostituendo l’Eq. 3 nell’Eq. 1, otteniamo: 
(4)
Moltiplicando entrambi i membri per ΦT otteniamo:
(5)
(6)
In cui C* è la matrice di smorzamento, Ω è chiamata matrice spettrale e Γ è il vettore contenente i fattori di partecipazione.
La massa eccitata dal moto è:
(7)
Il fattore di partecipazione è:
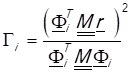(8)
La massa eccitata dall’i-esimo modo è:
(9)
Infine, la percentuale di massa partecipante (Eq. 9) è, se i modi sono normalizzati in massa:
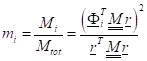(10)
L’analisi dinamica modale è adatta a tutti i tipi di struttura, regolari e non.